KeywordsBond Valuation Credit Risk Default Probability Default Risk Optimization Rating Migration
JEL Classification G32, G12
This paper has previously been included in an open access repository – SSRN.
Full Article
1. Introduction
1.1. The Factors Impacting Bond Valuation
The extent by which credit risk explain bond premiums is a predominant topic in bond valuation research. A number of authors conclude that it only accounts for a small fraction of bond premiums (Huang and Huang, 2012; Geske and Delianedis, 2001; Elton et al, 2001).
The predominant factors affecting bond prices are listed as risk free rates, taxes, jumps, liquidity, market risk factors, issue traits, equity volatility, market risk, systematic risk, and macroeconomic risk factors (Houweling et al, 2005; Geske and Delianedis, 2001; Elton et al, 2004; Elton et al, 2001; Grandes and Peter, 2005; Delianedis and Geske, 2003; Campbell and Taksler, 2003; Collin-Dufresne et al. 2001; Athanassakos and Carayannopoulos, 2001; Fama and French, 1993; Merton, 1974).
A number of studies also look at credit rating migration risk, or simply credit migration risk. Das and Tufano (1995) state investors are exposed to three risks: interest rate risk, changes in credit risk caused by changes in the credit rating of the issuer of the debt, and changes in credit risk caused by changes in spreads on the debt, even when ratings have not changed. Altman (1996) examines the expected spread change and cost implication due to credit rating migration. In the context of portfolios, Fei et al. (2012) note that risk models generally predict for each asset in the portfolio, the corresponding probability of default (PD), exposure at default (EAD) and loss given default (LGD). Similarly, Kadam and Lenk (2008) note different estimates for risk capital, derived from loss distributions, which they quantify as Value-at-Risk (VAR) and Expected Loss (EL) for the portfolio at hand. Jarrow et al. (1997) models the impact in forward rates – and thus bond value – due to credit rating jumps.
Delianedis and Geske (2003) note that default probabilities and changes in expected default frequencies are important to both the structure and pricing of credit derivatives. All corporate issuers have some positive probability of default. This default probability should change continuously with changes in the firm’s stock price and thus its leverage. The value of most fixed income securities is typically inversely related to the probability of default. Investors are concerned about changes in the value of their fixed income securities due to changes in the probability of default, even though the actual default seldom occurs. In fact, fixed income investors may be more concerned with changes in the perceived credit quality of their bond holdings than with actual default. Rating migrations, which offer one reflection of changes in perceived quality of bonds, occur much more frequently than defaults.
Foss (1995) specifically differentiates between credit risk and default risk. He notes that the terms default risk and credit risk are often used interchangeably; however, they are not one and the same. Default risk is defined as the risk that the issuer of a fixed-income security will be unable to make timely payments of interest or principal. This risk, diversified over a portfolio of equally rated securities, leads to an expected default loss. Many of the initial studies on risks and returns focus on historical default rates and losses. Although these studies provide valuable insight, default rates and default losses, in isolation, are not paramount. Credit risk is defined as the risk that the perceived credit quality of an issuer will change, although default is not necessarily a certain event. Increased credit risk is reflected in a widening of the yield spread. Credit and default risk are correlated because credit deterioration is almost always a precursor to eventual default; even in the most drastic cases, however, until default actually occurs, the potential for recovery or stabilization cannot be totally discounted. In line with this, Manzoni (2004) makes the point that, while several studies model default and bankruptcy events, no empirical work directly models the probability of a bond having its rating revised. He points out the traditional default mode of thinking of most financial institutions, leading to a consensus view of transitions as non-fundamental economic events.
1.2. Credit Default Swaps and Bond Valuation
Norden and Weber (2009) argue that CDS should reflect pure issuer default risk, and no facility or issue specific risk, making these instruments a potentially ideal benchmark for measuring and pricing credit risk. According to Blanco et al. (2005), CDSs are an upper bound on the price of credit risk (while credit spreads form a lower bound). Benkert (2004) argues that CDS premia represent primarily a price of default risk, and are in this respect similar to bond spreads. Consequently, CDS premia and bond spreads should be driven by the same factors. A number of studies (Benkert, 2004; Ericsson et al, 2009) indeed consider the same factors of bond valuation to explain CDS premiums. Weistroffer et al. (2009) mention that rating agencies use information derived from CDS prices to calculate market implied ratings.
1.3. Default Probability
Zhu (2006) states that, in general, measures of credit risk consist of three building blocks: probability of default (PD), loss given default (LGD) and correlation between PD and LGD. In order to model default risk, Athanassakos and Carayannopoulos (2001), consider three proxy variables: i) credit rating, which captures the effect of both the probability of default and the recovery rate; ii) time to maturity; iii) the existence of a sinking fund. Both of the latter two proxies should be related to the probability of default.
Grandes and Peter (2005) note that, when government bonds are not truly risk-free, particularly in an emerging market, the corporate yield spread above an equivalent government bond yield does not reflect corporate default risk, even after controlling for all other factors. It merely reflects corporate default risk in excess of sovereign default risk. They model corporate default probability as the probability that the firm defaults given that the sovereign does not default, plus the probability that the firm defaults given that the sovereign has defaulted.
Campbell and Taksler (2003) note that the literature distinguishes between structural and reduced form models. In structural models, a firm is assumed to default when the value of its liabilities exceeds the value of its assets, in which case bondholders assume control of the company in exchange for its residual value. Reduced form models, by contrast, assume exogenous stochastic processes for the default probability and the recovery rate. The added flexibility of the reduced-form approach allows default risk to play a somewhat greater role in the pricing of corporate bonds.
Merton (1974) shows that for a given maturity, the risk of default varies directly with the variance of the returns on the firm value. In this context, the business cycle and economic environment impact both the level of the risk free rate and the variance of returns on the firm value.
Huang and Huang (2012) consider a credit risk model with a counter-cyclical market risk premium to capture the effects of business cycles on credit risk premia. Secondly, they introduce an analytically tractable jump-diffusion structural credit risk model to capture the effects on credit risk premia of certain future states with both high default risks and abnormally high stochastic discount factors. The second mechanism is distinctly different from the first mechanism. In the model with jumps in asset values, the jumps are unpredictable and there is no time variation in market risk premia.
In line with reduced form models, Elton et al. (2001) develop marginal default probabilities from a rating transition matrix employing the assumption that the rating transition process is stationary and Markovian. In year one, the marginal probability of default can be determined directly from the transition matrix and default vector, and is, for each rating class, the proportion of defaults in year one. To obtain subsequent year defaults, they first use the transition matrix to calculate the ratings going into a given year for any bond starting with a particular rating in the previous year. The defaults of that year are then the proportion in each rating class multiplied by the probability that a bond in that class defaults by year end. They find that the marginal probability of default increases for the high-rated debt and decreases for the low-rated debt. This occurs because bonds change rating classes over time.
A number of studies use bond valuation models – both structural and reduced form – to note the extent by which market prices can be modelled, and to note the magnitude of default probability as bond valuation factor (Eom et al, 2004; Elton et al, 2001; Huang and Huang, 2012; Geske and Delianedis, 2001; Collin-Dufresne et al, 2001).
Fei et al. (2012) note a credit rating is a financial indicator of an obligor’s level of creditworthiness. Given the relationship between credit ratings and default probability or credit quality, Kumar and Haynes (2003) discuss rating methodology and list the key factors considered as: i) business analysis (industry risk; market position; operating efficiency; legal position), ii) financial analysis (accounting quality; earnings protection; adequacy of cash flows; financial flexibility; interest and tax sensitivity), and iii) management evaluation (track record of management; evaluation of capacity to overcome adverse situations; goals, philosophy and strategies). They find that financial parameters reflect, to a significant extent, the subjective and objective factors used by an expert while rating a debt obligation, with hidden relationships between the financial parameters and associated expert rating.
A number of authors examine the timeliness, accuracy and actual information content of credit rating agencies' ratings (Hines et al, 1975; Ederington and Goh, 1998; Amato and Furfine, 2004). Amato and Furfine (2004) mention that rating agencies insist that their ratings should be interpreted as ordinal rankings of default risk that are valid at all points in time, rather than absolute measures of default probability that are constant through time. Delianedis and Geske (2003) note that rating agencies regularly measure the historical default frequency of corporate issuers. While these historical default frequencies are interesting, they are not forward-looking. Option models can provide a forward-looking, risk neutral default probability. Chan and Jegadeesh (2004) point to evidence that agency ratings may not be accurate in a timely fashion.
Studies like Wang (2004) attempt to model default ratings, and studies like Hines et al. (1975), Kaplan and Urwitz (1979), Belkaoui (1980) and Chan and Jegadeesh (2004) statistically model bond ratings. This may provide alternative default probability estimates, as structural models also do, relative to the credit ratings of credit rating agencies, but must still be translated to default probability term structures, in a similar way credit agencies' ratings are translated.
Also, a number of studies quantify credit ratings as proxies of credit quality in terms of spread (Foss, 1995; Kaplan and Urwitz, 1979; Cantor et al, 1997; Perraudin and Taylor, 2004; Chan and Jegadeesh, 2004).
1.4. Default Probability Term Structures
Altman (1989) notes that analysts have concentrated their efforts on measuring the default rate for finite periods of time – for example, one year – and then averaging the annual rates for longer periods.
Elton (1999) argues that realized returns are a very poor measure of expected returns and that information surprises highly influence a number of factors in an asset pricing model. He believes that developing better measures of expected return and alternative ways of testing asset pricing theories that do not require using realized returns have a much higher payoff than any additional development of statistical tests that continue to rely on realized returns as a proxy for expected returns. He argues that either there are information surprises that are so large or that a sequence of these surprises is correlated so that the cumulative effect is so large that they have a significant permanent effect on the realized mean. Furthermore, these surprises can dominate the estimate of mean returns and be sufficiently large that they are still a dominant influence as the observation interval increases. Thus, the difference between expected and realized returns is viewed as a mixture of two distributions, one with standard properties and the other that more closely resembles a jump process.
Duffie and Singleton (1999) state that, because of the possibility of sudden changes in perceptions of credit quality, particularly among low-quality issues such as Brady bonds, one may wish to allow for surprise jumps in default probability.
Nelson and Siegel (1987) state the range of shapes generally associated with interest rate term structures: monotonic, humped, and S shaped. Related to this, a number of studies consider the relationship or correlation between default probability, interest rates, and the state of the economy (Benkert, 2004; Duffie and Singleton, 1999; Das and Tufano, 1995; Huang and Huang, 2012; Athanassakos and Carayannopoulos, 2001; Amato and Furfine, 2004; Delianedis and Geske, 2003; Longstaff and Schwartz, 1995; Kim et al. 1993; Campbell and Taksler, 2003; Lando and Skødeberg, 2002; Hamilton and Cantor, 2004).
Benkert (2004) argue that corporate defaults occur more often during economic downturns than during boom phases, and the occurrence of a recession may cause a decline in credit quality that leads to more defaults in the future. According to this line of reasoning, the compensation for default risk would rise. Duffie and Singleton (1999) note strong evidence that hazard rates for default of corporate bonds vary with the business cycle. Equally, recovery data also exhibit a pronounced cyclical component. Das and Tufano (1995) allowed recovery to vary over time so as to induce a non-zero correlation between credit spreads and the riskless term structure. However, for computational tractability they maintained the assumption of independence of the hazard rate (default rate) and risk-free rate.
Huang and Huang (2012) argue that a credit risk premium is required by investors because the uncertainty of default loss should be systematic – bondholders are more likely to suffer default losses in bad states of the economy. Moreover, precisely because of the tendency for default events to cluster in the worst states of the economy, the credit risk premium can be potentially very large. Athanassakos and Carayannopoulos (2001) note that yield spreads are greater during recessions than during recoveries, and also point to the link between the behaviour of yield spreads to the shape of the term structure, as a proxy of the business cycle. They confirm the typical direct relationship between default risk and yield spreads, and show that the impact of the business cycle (macro-economy) on the yield spread of a corporate bond depends on the industry sector to which the issuer of the bond belongs. The inflation rate should be directly related to yield spreads, since during inflationary periods investors may require higher risk premia from their investments in corporate bonds.
Athanassakos and Carayannopoulos (2001) use the change in the shape of the term structure of interest rates – represented by the quarterly change in the difference between the 20-year treasury rates and the three month t-bill rates – as a proxy for the business cycle, since much research in the past has linked the shape of the treasury term structure to future variations in the business cycle. A steepening term structure is a typical result of robust economic growth and lower short term interest rates and reflects a general belief in a more robust economic future. The opposite is true when the term structure is flattening or turns negatively sloped. Therefore, the particular proxy should be negatively related to yield spreads. Finally, the annual rate of change in the industrial production index should be negatively related to yield spreads since increased economic activity will bolster investors’ confidence in the corporate sector, and lead to a reduction in the risk premia demanded for investment in corporate bonds.
Amato and Furfine (2004) argue that financial market participants behave as if risk is countercyclical, e.g. at its highest during economic downturns. Empirical models, too, tend to indicate a rise in risk during recessions. There is a relationship between the correlation of default rates and loss in the event of default and the business cycle. Models that assume independence of default probabilities and loss given default will tend to underestimate the probability of severe losses during economic downturns. They delineate the empirical significance of the procyclicality of credit quality changes by showing that estimated credit losses are much higher in a contraction relative to an expansion.
Longstaff and Schwartz (1995) argue that the corporate yield spread should vary inversely with the benchmark treasury yield, and find evidence to support this. Kim et al. (1993) show that default risk is not particularly sensitive to the volatility of interest rates but is sensitive to interest rate expectations. Campbell and Taksler (2003) note idiosyncratic volatility can move very differently from market-wide volatility. Movements in idiosyncratic risk are more persistent than movements in market risk. Lando and Skødeberg (2002) note that it is likely that macroeconomic variables or other indicators of the business cycle influence rating intensities.
A number of studies model default probability term structures as instantaneous stochastic processes (Das and Tufano, 1995; Duffee, 1999; Jarrow et al, 2002) . For example, Duffee (1999) uses the extended Kalman filter to fit yields on bonds issued by individual investment-grade firms to a model of instantaneous default risk. Das and Tufano (1995) and Jarrow et al. (1997) model default risk as Markov chains or trees. Jarrow and Turnbull (1995) exogenously specify a stochastic process for the evolution of the default-free term structure and the term structure for risky debt.
Duffee (1999) argues that at each instant there is some probability that a firm defaults on its obligations. Both this probability and the recovery rate in the event of default may vary stochastically through time. The stochastic processes determine the price of credit risk. Although these processes are not formally linked to the firm's asset value, there is presumably some underlying relation. The instantaneous probability that a given firm defaults on its obligated bond payments follows a translated single-factor square-root diffusion process, with a modification that allows the default process to be correlated with the factors driving the default-free term structure. Realistically there are a number of factors other than default risk that drive a wedge between corporate and Treasury bond prices, such as liquidity differences, state taxes, and special repo rates. Here, all of these factors are substituted into a stochastic process called a default risk process. Default risk is negatively correlated with default-free interest rates. In addition, for the typical firm, the instantaneous risk of default has a lower bound that exceeds zero. In other words, even if a firm's financial health dramatically improves, the model implies that yield spreads on the firm's bonds remain positive.
Duffee (1999) first models the price of a risk-free bond as given by the expectation, under the equivalent martingale measure, of the cumulative discount rate between t and T. The discount rate follows a stochastic process – the sum of a constant, and two factors that follow independent square-root stochastic processes. He then models the adjusted discount rate for bond issues that can default, relative to risk-free bonds. This setup is designed to capture three important empirical features of corporate bond yield spreads. The most obvious is that the spreads are stochastic, fluctuating with the financial health of the firm. The second feature is that yield spreads for very high-quality firms are positive, even at the short end of the yield curve. This fact suggests that regardless of how healthy a firm may seem, there is some level below which yield spreads cannot fall. The third feature is that yield spreads, especially spreads for lower quality bonds, appear to be systematically related to variations in the default-free term structure.
Houweling and Vorst (2005) note reduced form models that use time series estimation to model the hazard rate stochastically, typically as a Vasicek or CIR process. Also, other reduced form models use cross-sectional estimation and consider either constant or stochastic hazard rates, where the stochastic process is chosen in such a way that the survival probability curve is known analytically. Houweling and Vorst (2005) follow an intermediate approach by using a deterministic function of time to maturity. This specification facilitates parameter estimation, while still allowing for time-dependency. They model the integrated hazard function as a polynomial function of time to maturity, with three degrees – linear, quadratic and cubic.
Das and Tufano (1995) choose to make recovery rates correlated with the term structure of interest rates. This results in a model wherein credit spreads are correlated with interest rates, as is evidenced in practice. In the Jarrow-Lando-Turnbull model credit spreads change only when credit ratings change, whereas in the debt markets it is found that credit spreads change even when ratings have not changed. Injecting stochastic recovery rates into the model provides this extra feature.
In the context of default probability term structures, credit migration and credit migration matrices should also be mentioned.
A number of studies examine the stochastic processes associated with rating transitions (Frydman and Schuermann, 2008; Lando and Skødeberg, 2002; Hamilton and Cantor, 2004; Altman, 1996). Altman and Rijken (2004) investigate the through-the-cycle methodology that agencies use, in the context of bond valuation, and rating timeliness and rating stability.
Nickell et al. (2000) use Moody’s data from 1970 to 1997 to examine the dependence of ratings transition probabilities on industry, country and stage of the business cycle using an ordered probit approach, and they find that the business cycle dimension is the most important in explaining variation of these transition probabilities. They point out that rating transition matrices vary according to the stage of the business cycle, the industry of the obligor and the length of time that has elapsed since the issuance of the bond. Kadam and Lenk (2008) identified strong differences in rating migration behaviour between issuers of different industry sectors and countries.
Bangia et al. (2002) argue that credit migration matrices provide the specific linkage between underlying macroeconomic conditions and asset quality. Credit migration matrices characterize the expected changes in credit quality of obligors. Total volatility (risk) is composed of a systematic and an idiosyncratic component. Because ratings are a reflection of a firm’s asset quality and distance to default, a reasonable definition of “systematic” is the state of the economy. They find distinct differences between the U.S. expansion and contraction transition matrices. The most striking difference between expansion and contraction matrices are the downgrading and especially the default probabilities that increase significantly in contractions. Overall, these results reveal that migration probabilities are more stable in contractions than they are on average, supporting the existence of two distinct economic regimes. The rating universe should develop differently in contraction periods compared to expansion times.
The straightforward application of these matrices however would normally be restricted to situations where the future state of the economy over the transition horizon under consideration is assumed to be known. The state of the economy clearly is one of the major drivers of systematic credit risk, especially as lower credit classes are much more sensitive to macro-economic factors. Consequently it should be integrated into credit risk modeling whenever possible, otherwise the downward potential of high-yield portfolios in contractions might be severely underestimated. Modern credit risk models account for different industries only through different term structures, but not through industry dependent transition matrices.
Fei et al. (2012) proposes an approach to estimate credit rating migration risk that controls for the business-cycle evolution during the relevant time horizon in order to ensure adequate capital buffers both in good and bad times. The approach allows the default risk associated with a given credit rating to change as the economy moves through different points in the business cycle. They mention a body of research linking portfolio credit risk with macroeconomic factors showing, for instance, that default risk tends to increase during economic downturns. Their premise is that point-in-time methodologies that account for business cycles should provide more realistic credit risk measures than through-the-cycle models that smooth out transitory fluctuations (perceived as random noise) in economic fundamentals.
1.5. Decomposing Default Probabilities from Market Data
1.5.1. Decomposing Rating Migration Matrices from Market Data
Taken from Barnard (2017), equation 1 states the reduced form model of Duffie and Singleton (1999), adapted for coupon paying bonds. Equation 1 has two components, a coupon paying component associated with non-default outcomes, and a recovery component associated with default outcomes.
In the equation, ![]() is the price or value of the risk-bearing bond;
is the price or value of the risk-bearing bond; ![]() is the number of coupons of the bond, including par;
is the number of coupons of the bond, including par; ![]() is the coupon of the bond on coupon date
is the coupon of the bond on coupon date ![]() ;
; ![]() is the recovery of par value;
is the recovery of par value; ![]() and
and ![]() are the risk-free spot rate and time value, respectively, associated with coupon date
are the risk-free spot rate and time value, respectively, associated with coupon date ![]() ;
; ![]() is the default probability of interval
is the default probability of interval ![]() , conditional on no default prior to interval
, conditional on no default prior to interval ![]() ;
; ![]() is the cumulative non-default probability of interval
is the cumulative non-default probability of interval ![]() ;
; ![]() is the number of probability intervals for which the possibility of default is considered up to coupon date
is the number of probability intervals for which the possibility of default is considered up to coupon date ![]() ;
; ![]() is the number of probability intervals considered up to maturity.
is the number of probability intervals considered up to maturity.
For coupon paying bonds, it is convenient to consider ![]() and
and ![]() to be equal to
to be equal to ![]() and
and ![]() . For example, the third coupon may have three probability intervals leading up to it. For zero-coupon bonds,
. For example, the third coupon may have three probability intervals leading up to it. For zero-coupon bonds, ![]() is equal to 1, and
is equal to 1, and ![]() may be greater than
may be greater than ![]() , with
, with ![]() not necessarily corresponding with
not necessarily corresponding with ![]() ; a regular coupon interval may still be considered though to ensure a timely and consistent consideration of default. A five-year zero coupon bond will have only one coupon, but can have up to ten probability intervals leading up to it, if semi-annual probability intervals are used.
; a regular coupon interval may still be considered though to ensure a timely and consistent consideration of default. A five-year zero coupon bond will have only one coupon, but can have up to ten probability intervals leading up to it, if semi-annual probability intervals are used.
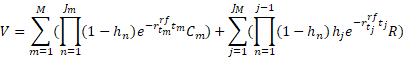
|
[1.1] |
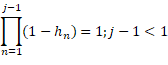
|
[1.1.1] |

|
[1.2] |
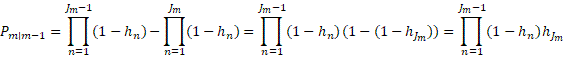
|
[1.3] |
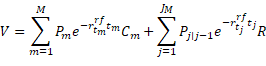
|
[1.4] |
Although not explicitly stated by them, equation 2 delineates the default probability structure implemented by Elton et al. (2001). They subsequently substitute this into a reduced form model similar to equation 1.
![]() are all non-default rating categories;
are all non-default rating categories; ![]() is the intensity or propensity of path or tree
is the intensity or propensity of path or tree ![]() that leads up to interval
that leads up to interval ![]() ; similarly,
; similarly, ![]() is the path intensity or propensity of path
is the path intensity or propensity of path ![]() ;
; ![]() is the intensity or propensity of rating category
is the intensity or propensity of rating category ![]() in interval
in interval ![]() ;
; ![]() is the number of default paths of (up to) interval
is the number of default paths of (up to) interval ![]() ;
; ![]() is the number of non-default paths of interval
is the number of non-default paths of interval ![]() ; contrary to a default path, a non-default path can not and does not end up in default over its length or run;
; contrary to a default path, a non-default path can not and does not end up in default over its length or run; ![]() is the number of non-default paths that migrate to – end with – category
is the number of non-default paths that migrate to – end with – category ![]() in interval
in interval ![]() ;
; ![]() is the probability of migration from rating
is the probability of migration from rating ![]() in interval
in interval ![]() to rating
to rating ![]() in interval
in interval ![]() ;
; ![]() is the probability of migration from category
is the probability of migration from category ![]() to category
to category ![]() in interval
in interval ![]() ;
; ![]() is the probability of category
is the probability of category ![]() migrating to default status in interval
migrating to default status in interval ![]() ;
; ![]() is again the default probability of interval
is again the default probability of interval ![]() , conditional on no default prior to interval
, conditional on no default prior to interval ![]() .
.
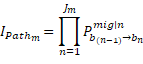
|
[2.1] |
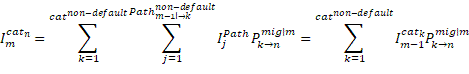
|
[2.2] |
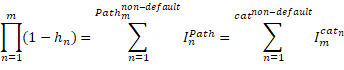
|
[2.3] |
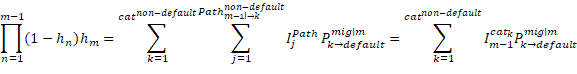
|
[2.4] |
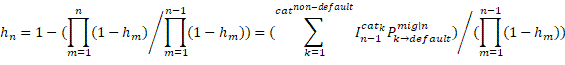
|
[2.5] |
Equation 3 allows the recovery rate to depend on the rating category the bond is in when it defaults. Moving from equation 1.4 to equation 3.1 is further explained by equation set 2. ![]() is the recovery of par value of rating category
is the recovery of par value of rating category ![]() in interval
in interval ![]() .
.
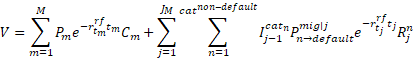
|
[3.1] |
Equation set 4 contains the optimization problem to extract the market rating migration matrix from market prices. Any proper rating migration matrix that satisfy the constraints could serve as initial solution. The probabilities of the migration matrix form the coefficients of the optimization problem and are adjusted and selected as part of the optimization. A number of constraints can be stipulated, varying in principality or importance: For each rating category, the sum of the probabilities of migrating from the particular category to any other non-default category, plus the probability of default of the category should equal 1 (equation 4.b). For each rating category, any probability of migrating to any other non-default category, as well as the probability of default of that particular category should be greater than or equal to zero (equation 4.c). For each rating category with a rating category preceding it, the particular category's probability of default should be equal to or higher than that of the category preceding it (equation 4.d). For each rating category, the probability of migrating to rating category ![]() is equal to or greater than the probability of migrating to rating category
is equal to or greater than the probability of migrating to rating category ![]() or
or ![]() (equation 4.e).
(equation 4.e).
![]() and
and ![]() are the market and modelled bond value of bond
are the market and modelled bond value of bond ![]() ;
; ![]() and
and ![]() are the market and modelled bond value of bond
are the market and modelled bond value of bond ![]() with rating category
with rating category ![]() ;
; ![]() is the total number of bonds included in the sample;
is the total number of bonds included in the sample; ![]() is the total number of sample bonds of rating category
is the total number of sample bonds of rating category ![]() ;
; ![]() refers to all the non-default rating categories;
refers to all the non-default rating categories; ![]() is the probability of migrating from category
is the probability of migrating from category ![]() to
to ![]() ;
; ![]() is the probability of default for category
is the probability of default for category ![]() .
.
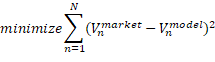
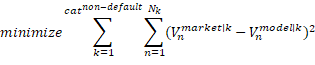
|
[4.a] | |
| Subject to: | ||
|
|
[4.b] | |
|
|
[4.c] | |
|
|
[4.d] | |
|
|
|
[4.e] |
Equation 4.b forms an equality constraint – for any rating category, the sum of the probabilities of migrating from the particular category to any other non-default category, plus the probability of default of the category should at all times equal 1. A principal concern is the integrity of partial derivatives measured during optimization, in the wake of this equality constraint – given the way partial derivatives are measured during optimization, it may essentially imply non-conformance to or a relaxation of the equality constraint, and it may in turn imply the partial derivatives measured are distorted. If the equality constraint must be met not to distort the measurement of partial derivatives of the migration probability coefficients, it implies the basic assumption of coefficient independence does not hold. Thus, it becomes a question of whether it is permissible to assume coefficient independence during measurement of partial derivates as part of optimization.
In light of this, it is suggested that, instead of modelling and optimizing migration probability coefficients directly, delta coefficients are rather used to model and optimize rating category migration probabilities. For this purpose, all rating migrations are sub-classified as primary or x-to-x migration, and secondary or x-to-y migration. Primary or x-to-x migration involves the particular rating category maintaining its rating; secondary or x-to-y migration involves the rating category migrating to a different rating category, including default. A particular delta coefficient then depicts the net movement or change between the primary or x-to-x migration and the corresponding secondary or x-to-y migration of the associated rating category. Therefore, only x-to-y migration probabilities are assigned delta coefficients. The intermediate or end value of any x-to-y migration probability equals its initial value – emanating from the initial solution – plus its delta coefficient (equation 5.a). x-to-x migration probabilities are not assigned delta coefficients directly, but obtain their intermediate and end values from the sum of the x-to-y migration delta coefficients (equation 5.b), that can also be seen as depicting net movement out of the primary migration probability coefficient. In other words, according to equation 5, a positive delta coefficient implies x-to-x migration increases, and the corresponding x-to-y migration decreases, and vice versa. This way, the mentioned equality constraint is met at all times, also when measuring partial derivatives.
![]() is the initial rating migration probability;
is the initial rating migration probability; ![]() is the end rating migration probability;
is the end rating migration probability; ![]() is the rating migration delta between primary rating category
is the rating migration delta between primary rating category ![]() and secondary rating category
and secondary rating category ![]() ;
; ![]() and
and ![]() depict x-to-y migration of rating category
depict x-to-y migration of rating category ![]() ;
; ![]() depict x-to-x migration of rating category m.
depict x-to-x migration of rating category m.
|
|
[5.a] |
|
|
[5.b] |
Equation 6 rewrites the original optimization problem in terms of delta coefficients.
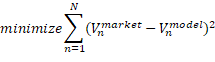
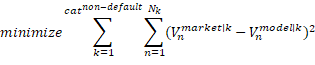
|
[6.a] | |
| Subject to: | ||
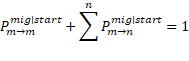
|
|
[6.b] |
|
|
|
[6.c] |
|
|
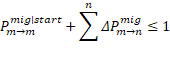
|
[6.d] |
|
|
[6.e] | |
|
|
[6.f] | |
|
|
[6.g] | |

|
[6.h] | |

|
[6.i] | |
1.5.2. Decomposing Default Probability Structures from Market Data
Equation 4 and 6 may still be complex, computationally expensive, and may still be improved upon, particularly with improved initial solutions. One option may be to first decompose default probability term structures per rating category, and then to decompose or work towards a rating migration matrix from this. Equation 7 stipulates the optimization problem to decompose default probability term structures from market data for rating categories. The constraints are that each of the interval default probabilities must be greater than or equal to 0, and less than or equal to 1 (equation 7.b). Also, a constraint is added to limit the resulting structure variance below a stipulated ceiling (equation 7.c). This method of decomposition is outlined by Barnard (2016a) and Barnard (2016b). Structure variance is measured as the rate of change of interval default probability. Modelled bond value is based on the reduced form model of equation 1, and the interval default probabilities decomposed are substituted into that equation.
Again, ![]() and
and ![]() are the market and modelled bond value of bond
are the market and modelled bond value of bond ![]() with rating category
with rating category ![]() ;
;![]() is the total number of sample bonds of rating category
is the total number of sample bonds of rating category ![]() ;
; ![]() is the interval default probability of interval
is the interval default probability of interval ![]() ;
; ![]() is the total number of intervals;
is the total number of intervals; ![]() is the specified variance ceiling.
is the specified variance ceiling.
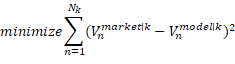
|
[7.a] | |
| Subject to: | ||
|
|
|
[7.b] |
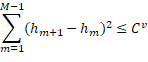
|
[7.c] | |
As part of the optimization, market bond value – as opposed to modelled bond value – can also be based on a market based interest rate term structure instead – an interest rate term structure decomposed from market data. Instead of its quoted price, the market value of a bond is taken to be the resultant value when discounting the bond against the market based interest rate term structure. This assumes the decomposed market interest rate term structure ideally represents the market outlook, and this renders issues' residual modelling error equal to zero. The benefit of this is that it reduces idiosyncratic bond value error, therby simplifying the problem. This also shifts the focus from merely a portfolio of bonds to an interest rate term structure instead, such that the objective is expressed as decomposing the corresponding default probability structure of an interest rate term structure, and vice versa, rather than decomposing the default probability structure of a portfolio.
Furthermore, when market bond value is based on a decomposed interest rate term structure, and the number of issues are sufficient, and adequately spaced in terms of maturity, it is also possible to calculate a default probability term structure by means of a sequential (bootstrapping) method that iteratively seeks the next interval default probability that minimizes modelled issue value error. The mechanics of the sequential method is easy to follow when considering an issue with such a maturity that it is only affected by one interval default probability – in this case, the default probability structure (applicable to the issue) only spans one interval, and can be calculated through iterative searching. When ordering issues according to maturity, each subsequent issue will then also have only one outstanding interval default probability, if it adopts the default probability structure of the preceding issues and intervals.
2. Methodology
The study examines the power and accuracy of the proposed method to decompose default probability term structures from market data, and in particular from interest rate term structures decomposed from market data. In particular, the study examines the corresponding interest rate term structures of the default probability term structures of a typical rating migration matrix. Also, the study examines the default probability term structures of interest rate term structures, firstly those obtained from the previous step – mapping the interest rate term structures obtained from the default probability term structures of the rating migration matrix back to default probability term structures – and secondly a typical market interest rate term structure set. In addition, the study examines the extent by which it is possible to utilize external (artificial) bond portfolios as part of decomposing default probability term structures, by examining the sensitivity of the results to the coupon rates of the bond portfolio sample used as part of the study.
Overall, seven principal credit ratings are considered – [AAA, AA, A, BBB, BB, B, CCC]. In all cases that bond value is modelled, equation 1 is used to calculate the value of the bonds. For this purpose, recovery rates are taken from Elton et al. (2001). Table 1 shows the recovery rates used. In all cases, the risk-free rate used is taken from Elton et al. (2001) and Huang and Huang (2012). Also, in all cases, an artificial portfolio of bonds is used. The coupons of the bonds are varied – four different values are used: 2.5, 5.0, 7.5, and 10.0. Ten intervals are considered, and the maturity of the issues are such that one issue matures per interval. Thus, 10 issues are used per rating category, and 70 issues are used overall.
The study uses a rating migration matrix from Elton et al. (2001) to map the interest rate term structures corresponding to the default probability term structures of this rating migration matrix. The rating migration matrix is slightly adapted where it violates some of the constraints mentioned as part of equation 4. Table 2 and table 3 show the original and adapted rating migration matrix, respectively. The default probability term structures of this particular rating migration matrix are substituted into equation 1 to calculate corresponding bond value. Interest rate term structures are then decomposed from this price data to obtain interest rate term structures for the default probability term structures. For this purpose, the decomposition method of Barnard (2016a) is used. In all cases, a structure variance ceiling of 0.001 or lower is used.
The interest rate term structures obtained for the default probability term structures of the above-mentioned rating migration matrix are again used as input, and their corresponding default probability term structures are decomposed to investigate the extent by which the original default probability term structures are again surfaced. In addition, risk-free and risk-bearing term structures from Elton et al. (2001) and Huang and Huang (2012) are used to examine the default probability term structures of typical market interest rate term structures. Figure 1 shows the risk-free and risk-bearing term structures. When decomposing the default probability term structures of interest rate term structures, the bonds are discounted against the applicable interest rate term structure and this price data is used. Both the optimization method and sequential method are used to decompose default probability term structures, and equation 1 is used to model bond value.
To implement the sequential (bootstrapping) method, a custom algorithm is written to sequentially calculate and iteratively search interval default probabilities. A simple barrier method is utilized to implement the optimization method. However, an algorithm is used to iteratively switch between optimization equations, and the best result per iteration is used as the initial solution of the next iteration. Equation 8 notes the optimization equations used, in extension to the least-squares problem expression of equation 7.a. Nevertheless, all optimization equation results are still converted to, expressed, and compared in terms of equation 7.a. Equation 8.c and equation 7.a are identical. Equation 8.b considers absolute modelling error, instead of squared modelling error, and equation 8.d and 8.e respectively penalize positive and negative modelling error more strongly.
|
|
[8.a] |
|
|
[8.b] |
|
|
[8.c] |
|
|
[8.d] |
|
|
[8.e] |
Table 1. Recovery rates as percentage of par (Elton et al, 2001)
| AAA | AA | A | BBB | BB | B | CCC |
| 68.34 | 59.59 | 60.63 | 49.42 | 39.05 | 37.54 | 38.02 |
Table 2. Rating migration probability – Standard and Poor's (Elton et al, 2001)
| AAA | AA | A | BBB | BB | B | CCC | Default | |
| AAA | 90.788 | 8.291 | 0.716 | 0.102 | 0.102 | 0.000 | 0.000 | 0.000 |
| AA | 0.103 | 91.219 | 7.851 | 0.620 | 0.103 | 0.103 | 0.000 | 0.000 |
| A | 0.924 | 2.361 | 90.041 | 5.441 | 0.719 | 0.308 | 0.103 | 0.103 |
| BBB | 0.000 | 0.318 | 5.938 | 86.947 | 5.302 | 1.166 | 0.117 | 0.212 |
| BB | 0.000 | 0.110 | 0.659 | 7.692 | 80.549 | 8.791 | 0.989 | 1.209 |
| B | 0.000 | 0.114 | 0.227 | 0.454 | 6.470 | 82.747 | 4.086 | 5.902 |
| CCC | 0.228 | 0.000 | 0.228 | 1.251 | 2.275 | 12.856 | 60.637 | 22.526 |
| Default | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 100.000 |
Table 3. Rating migration probability adapted from Standard and Poor's (Elton et al, 2001)
| AAA | AA | A | BBB | BB | B | CCC | Default | |
| AAA | 90.789 | 8.291 | 0.716 | 0.102 | 0.102 | 0.000 | 0.000 | 0.000 |
| AA | 0.103 | 91.22 | 7.851 | 0.620 | 0.103 | 0.103 | 0.000 | 0.000 |
| AAA | AA | A | BBB | BB | B | CCC | Default | |
| A | 0.924 | 2.361 | 90.041 | 5.441 | 0.719 | 0.308 | 0.103 | 0.103 |
| BBB | 0 | 0.318 | 5.938 | 86.947 | 5.302 | 1.166 | 0.117 | 0.212 |
| BB | 0 | 0.110 | 0.659 | 7.692 | 80.550 | 8.791 | 0.989 | 1.209 |
| B | 0 | 0.114 | 0.227 | 0.454 | 6.470 | 82.747 | 4.086 | 5.902 |
| CCC | 0.228 | 0.228 | 0.228 | 1.251 | 2.275 | 12.856 | 60.408 | 22.526 |
| Default | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 100.000 |
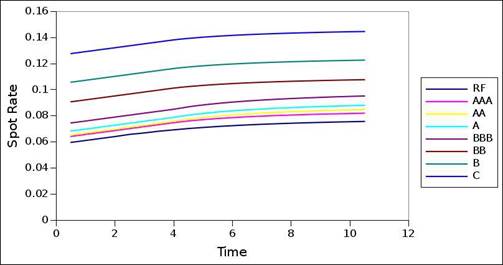
Figure 1. Risk-free and risk-bearing term structures
3. Analysis
Figure 2 to 8 show the interest rate term structures decomposed for the default probability term structures of the rating migration matrix (table 2). The corresponding default probability term structures of the rating migration matrix form the reference structures of figure 9 to 15, and can be seen in these figures. For all 7 rating categories, the 4 different coupon sizes were used to decompose the interest rate term structures, and the interest rate term structures of the different coupon sizes are delineated in the graphs. In all cases, residual modelling error is negligible (maximum error is measured at 1E-08, with most cases measuring error far less than 1E-08) and the decomposed interest rate term structures can thus be seen as accurate representations. In some of the cases, the decomposed term structure still carry some excess variation, and the term structures can be further optimized by further fine-tuning the variance ceiling. Regardless, the graphs reveal the fundamental structures.
Rating category C struggles to decompose an interest rate term structure, given the bond values stemming from the default probability term structure. The constant forward rate plots of figure 8 are the initial solutions used, and the optimization could not find better solutions in these cases. One viable conclusion then is that this particular default probability term structure of the rating migration matrix is partly invalid, from the point of view of a valid interest rate term structure, and constraints in this regard. One constraint in particular may be negative forward rates – the default probability term structure requires negative forward rates to decompose an interest rate term structure.
From a comparison between the default probability term structures and interest rate term structures, it is evident that the forward rates accelerates and decelerates according to and in accordance with the acceleration and deceleration of the default probability. The transition from default probability term structure to interest rate term structure is also sensitive to the magnitude of the coupons. However, the extent thereof differs across the rating categories, with the higher rating categories being less sensitive, and the lower rating categories being more sensitive. Nonetheless, general structure is seemingly perserved – even though the interest rate term structures of different coupon sizes differ for the same default probability structure, their structure is similar and comparable. Most of the sensitivity occurs across the tail of the term structure, with little sensitivity across the front of the term structure.
A question that naturally derives from this is the extent by which the interest rate term structures corresponding to the default probability term structures of typical rating migration matrices correspond to market interest rate term structures – do default probability term structures stemming from rating migration matrices and default probability term structures embedded in market data correspond then?
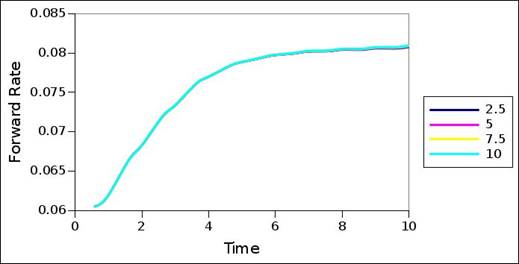
Figure 2. Forward rate interest term structure – AAA

Figure 3. Forward rate interest term structure – AA
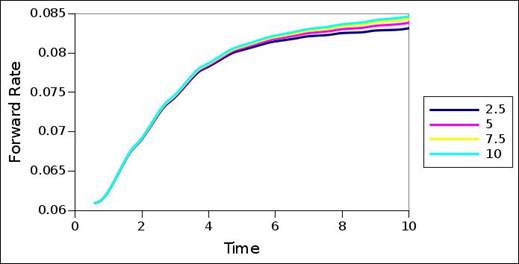
Figure 4. Forward rate interest term structure – A
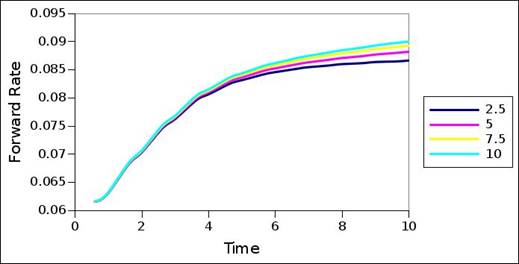
Figure 5. Forward rate interest term structure – BBB
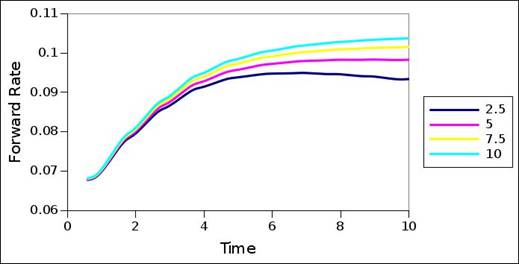
Figure 6. Forward rate interest term structure – BB
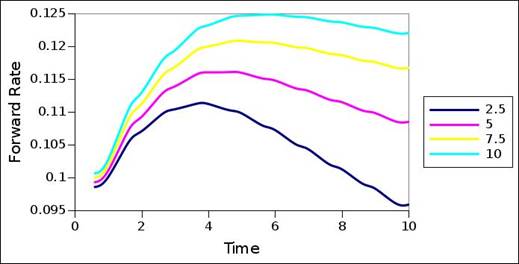
Figure 7. Forward rate interest term structure – B
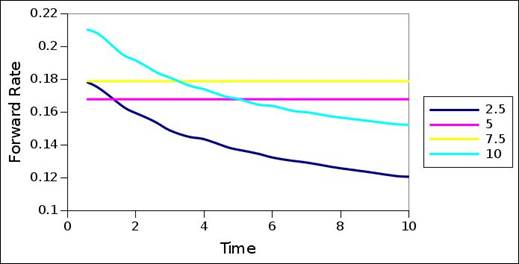
Figure 8. Forward rate interest term structure - CCC
Figure 9 to 15 show the resultant default probability term structures when again utilizing as input the decomposed interest rate term structures of the original default probability term structures of the rating migration matrix. Core to this inquiry is the extent by which the original default probability term structures can again be surfaced, as a method to reflect on model power, accuracy, and distortion or error. Given that 4 different coupon sizes were used during the previous test, the interest rate term structures corresponding to a coupon size of 7.5 are selected and used as the reference case here. Hence, the expectation is that the original default probability term structures of the rating migration matrix must again be sourced, when using a coupon size of 7.5, and when utilizing the interest rate term structures corresponding to a coupon size of 7.5, decomposed during the previous test. Nevertheless, the 4 different coupon sizes are again underlying the decompositions, to also note the sensitivity of the decomposed default probability term structures to coupon size. The figures show the default probability term structures corresponding to the different coupon sizes, together with the reference default probability term structure of the rating migration matrix.
The results show that the original default probability term structure is again surfaced in all cases, when the coupon size match – the default probability term structure corresponding to a coupon size of 7.5 perfectly lies on the reference default probability term structure. The exception is rating category CCC, which struggled to decompose an interest rate term structure in the first place. Again, the results are sensitive to the coupon size. However, this time the sensitivity is more constant across the different rating categories – both higher and lower rating categories reveal significant sensitivity, with less difference in sensitivity between higher and lower rating categories. Still, the term structures of the different coupon sizes are comparable. Sensitivity is again restricted to the tail of the term structures.

Figure 9. Default probability term structure - AAA
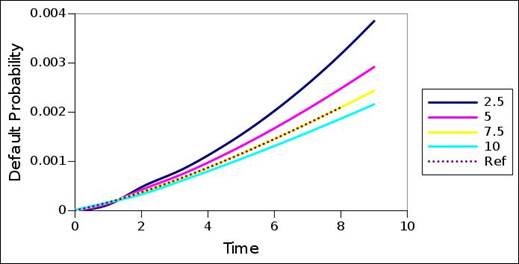
Figure 10. Default probability term structure – AA
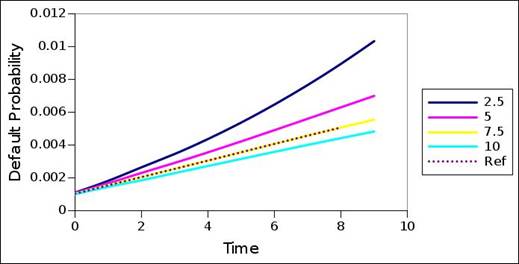
Figure 11. Default probability term structure – A

Figure 12. Default probability term structure – BBB
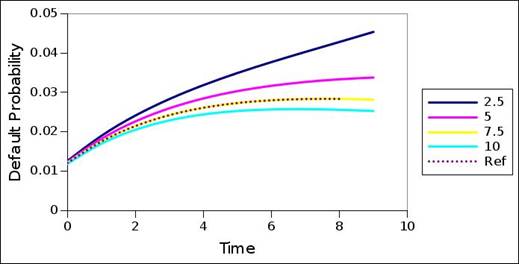
Figure 13. Default probability term structure – BB

Figure 14. Default probability term structure – B

Figure 15. Default probability term structure - CCC
Figure 16 to 22 show the default probability term structures corresponding to and decomposed from the market term structures of Figure 1. Again, this is done for the four different coupon sizes. Residual modelling error is insignificant. The structures are again sensitive to the coupon sizes, with the sensitivity consistent across the rating categories, and comparable structure prevailing across the different structures corresponding to the different coupon size.
The portfolio – and particularly the coupons – used may differ from the original market portfolio used to decompose these market interest rate term structures. Still, given basic structure consistency across the default probability term structures of different coupon sizes, a primary question is the extent by which these default probability term structures correspond with the default probability term structures of typical rating migration matrices. When compared to the default probability structures of the rating migration matrix of the previous test, the market based default probability term structures generally contain a greater constant component: in most (all) of cases, the market based default probability term structures have higher initiating values, that are generally maintained across the term structure. The intervals and nature of acceleration and deceleration also differ. The terminating values are generally higher in the case of the market based default probability term structures.
In addition, even when accounting for the impact of the coupon size, significant differences exist between the default probabilities emanating from the plots, and the default probabilities contained in the rating migration matrix (table 2). With reference to equation 1, 2 and 3, and with reference to interval rating category intensities due to rating migration propagation (Barnard, 2017), only the primary rating category has non-zero intensity in the first interval, and because of this, only the primary rating category contributes to migration to default in the first interval. As a consequence, all default migration of the first interval is attributable to the primary rating category, and corresponds to the default probability of the primary rating category. Thus, it allows a comparison between the rating migration matrix default probability entry of a particular rating category, and the first interval default probability from the default probability term structure of the rating category. Table 4 lists the differences
Table 4. Comparison of rating default probability – rating migration matrix versus decomposed default probability term structures
| Rating migration matrix default probability (%) (table 2) | Decomposed default probability term structure first interval default probability (%) (figure 16 – 22; approximate) | |
| AAA | 0.000 | 1.200 |
| AA | 0.000 | 1.200 |
| A | 0.103 | 2.000 |
| BBB | 0.212 | 3.000 |
| BB | 1.209 | 5.000 |
| B | 5.902 | 7.000 |
| CCC | 22.526 | 10.000 |
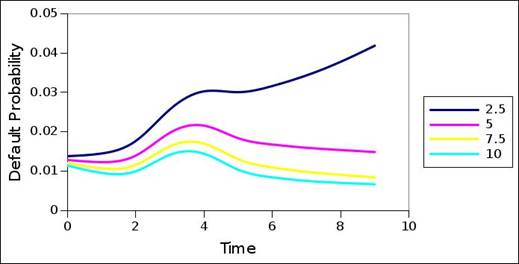
Figure 16. Default probability term structure of market interest rate term structure – AAA

Figure 17. Default probability term structure of market interest rate term structure – AA
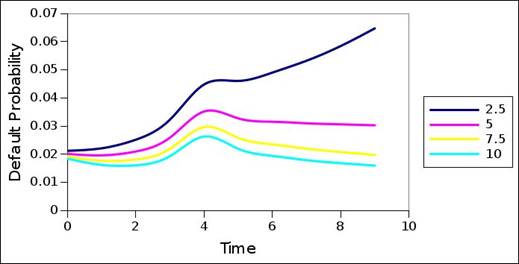
Figure 18. Default probability term structure of market interest rate term structure – A
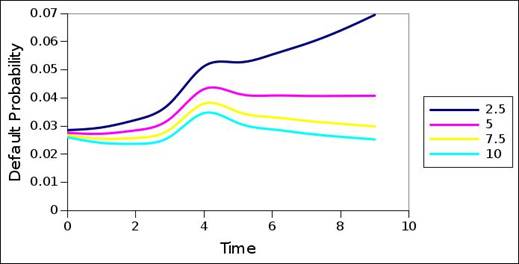
Figure 19. Default probability term structure of market interest rate term structure – BBB

Figure 20. Default probability term structure of market interest rate term structure – BB
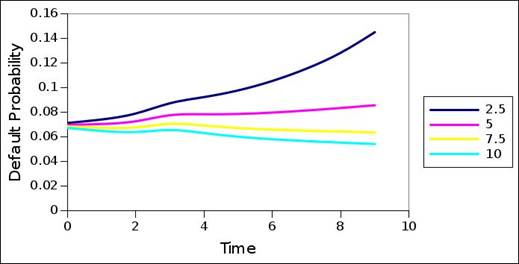
Figure 21. Default probability term structure of market interest rate term structure – B
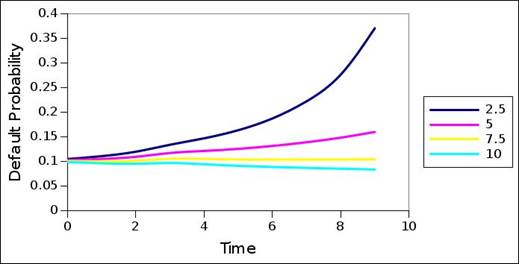
Figure 22. Default probability term structure of market interest rate term structure – CCC
Figure 23 to 24 compare the default probability term structures decomposed with the optimization method, and the default probability term structures decomposed with the sequential method, given the same sample bond portfolio, and for the market interest rate term structures. Here, a coupon size of 7.5 is used. In this case, the two methods yield identical results.

Figure 23. Comparison between optimization and sequential method – AAA to BBB
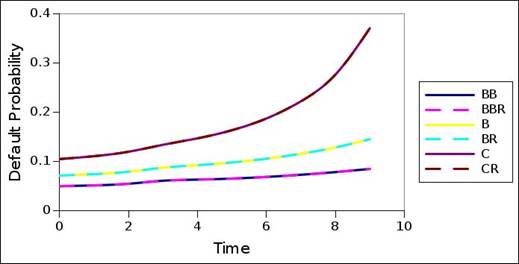
Figure 24. Comparison between optimization and sequential method – BB to CCC
4. Conclusion
Within the greater context and goal of decomposing rating migration matrices from market price data, two methods to decompose default probability term structures for rating categories from market data, were considered and empirically evaluated – an optimization method and a sequential method.
In principle, whenever it is possible to decompose an interest rate term structure for a rating category, it should also be possible to decompose a default probability term structure for the particular interest rate term structure of the rating category. In general, the prerequisites, particularly in terms of sample size, are comparable. Both zero-coupon and coupon bearing bonds can be used to decompose interest rate as well as default probability term structures. Here, both interest rate and default probability term structures were decomposed from a modest sample size, such that the number of issues (sample size) required is not necessarily a limiting factor.
It is demonstrated that the two models have comparable outputs. Yet, the optimization method should offer greater flexibility over the sequential method, in terms of issue maturity distributions. The optimization method does not necessarily require an issue to mature in each interval. Nevertheless, the sequential method is computationally less expensive, and when utilizing artificial and simulated portfolios, the sequential method can still be utilized to illuminate default probability term structures with a reasonable degree of accuracy. This by itself may be informative and can help to shape subsequent decompositions and inquiries.
Decompose default probability term structures from market data also allows a mapping between default probability term structures and interest rate term structures – the mapping of the default probability term structures of interest rate term structures, and vice versa. As a result, the immediate question emanating from this is whether decomposed default probability term structures are structurally valid and proper, and how it reflects on market interest rate term structures and market prices. In turn, this may imply and permit a useful evaluation tool – whether an interest rate (default probability) term structure is valid and sensible, when considering its corresponding default probability (interest rate) term structure, and vice versa.
For the data used, the default probability term structures decomposed from the market interest rate term structure set significantly differ from the rating migration matrix based default probability term structures. Of course, coupon size is a determining factor. Still, this factor alone can not account for the discrepancy. This then places focus on the comprehensiveness of the underlying bond valuation model. If the model is assumed to be sufficiently comprehensive, the conclusion is that market expectations of default probability differ from that of rating migration matrices, and the historical outcomes of default probability from which the rating migration matrix default probabilities are devised.
The underlying bond valuation model used as part of the decompositions did not include taxation as factor. This is something that can receive further attention. Still, a number of studies contest whether default is a prominent factor of bond valuation. This view may be premised on a presupposed model of default probability and default probability term structures. When decomposing default probability term structures from market data, fewer presuppositions are made, specifically given the way it is conducted. The results yield additional data that may require that the prominence of default probability as bond valuation factor should be reconsidered.
By nature, decomposed default probability term structures would move with market prices and market interest rate term structures, and whenever market prices and market interest rate term structures change. This too is an interesting dynamic to consider. It implies that default probability term structures move with greater frequency than what may be anticipated, and an implication may be that the price implications are already contained and incorporated into the default probability term structures, such that the default probability term structures also contain an embedded volatility component.
References
- Altman, E.I., 1989. Measuring corporate bond mortality and performance. The Journal of Finance, 44(4), pp. 909-922.
- Altman, E.I., 1996. Rating Migration of Corporate Bonds: Comparative Results and Investor/Lender Implication. NYU Working Paper.
- Altman, E.I. and Rijken, H.A., 2004. How rating agencies achieve rating stability. Journal of Banking & Finance, 28(11), pp.2679-2714.
- Amato, J.D. and Furfine, C.H., 2004. Are credit ratings procyclical?. Journal of Banking & Finance, 28(11), pp.2641-2677.
- Athanassakos, G. and Carayannopoulos, P., 2001. An empirical analysis of the relationship of bond yield spreads and macro economic factors. Applied Financial Economics, 11(2), pp.197-207.
- Bangia, A., Diebold, F.X., Kronimus, A., Schagen, C. and Schuermann, T., 2002. Ratings migration and the business cycle, with application to credit portfolio stress testing. Journal of Banking & Finance, 26(2), pp.445-474.
- Barnard, B., 2016a. Interest Rate Term Structure Decomposition: An Axiomatic Structural Approach [online] Available at: https://papers.ssrn.com/abstract=2847737 [Accessed on 3 May 2017].
- Barnard, B., 2016b. Interest Rate Term Structure Decomposition at the Instrument Level [online] Available at: https://papers.ssrn.com/abstract=2866995 [Accessed on 3 May 2017].
- Barnard, B., 2017a. Rating Migration and Bond Valuation: Towards Ahistorical Rating Migration Matrices and Default Probability Term Structures [online] Available at: https://papers.ssrn.com/abstract=2893521 [Accessed on 3 May 2017].
- Barnard, B., 2017b. Rating Migration and Bond Valuation: Ahistorical Interest Rate and Default Probability Term Structures [online] Available at: https://papers.ssrn.com/abstract=2948352 [Accessed on 3 May 2017].
- Belkaoui, A., 1980. Industrial bond ratings: A new look. Financial Management, pp.44-51.
- Benkert, C., 2004. Explaining credit default swap premia. Journal of Futures markets, 24(1), pp.71-92.
- Blanco, R., Brennan, S. and Marsh, I.W., 2005. An empirical analysis of the dynamic relation between investment‐grade bonds and credit default swaps. The Journal of Finance, 60(5), pp.2255-2281.
- Campbell, J.Y. and Taksler, G.B., 2003. Equity volatility and corporate bond yields. The Journal of Finance, 58(6), pp.2321-2350.
- Cantor, R., Packer, F. and Cole, K., 1997. Split ratings and the pricing of credit risk. The Journal of Fixed Income, 7(3), pp.72-82.
- Chan, K. and Jegadeesh, N., 2004. Market-based evaluation for models to predict bond ratings. Review of Pacific Basin Financial Markets and Policies, 7(02), pp.153-172.
- Collin‐Dufresne, P., Goldstein, R.S. and Martin, J.S., 2001. The determinants of credit spread changes. The Journal of Finance, 56(6), pp.2177-2207.
- Das, S., and Tufano, P., 1995. Pricing Credit Sensitive Debt When Interest Rates, Credit Ratings, and Credit Spreads Are Stochastic. Journal of Financial Engineering, 5, 161-198.
- Delianedis, G. and Geske, R.L., 2003, February. Credit risk and risk neutral default probabilities: information about rating migrations and defaults. In EFA 2003 annual conference paper (No. 962).
- Duffee, G.R., 1999. Estimating the price of default risk. Review of Financial Studies, 12(1), pp.197-226.
- Duffie, D. and Singleton, K.J., 1999. Modeling term structures of defaultable bonds. Review of Financial studies, 12(4), pp.687-720.
- Ederington, L.H. and Goh, J.C., 1998. Bond rating agencies and stock analysts: who knows what when?. Journal of Financial and Quantitative Analysis, 33(04), pp.569-585.
- Elton, J.E., 1999. Expected return, realized return and asset pricing tests. Journal of Finance, 4, pp.1199-1220.
- Elton, E. J., Gruber, M. J., Agrawal, D. and Mann, C., 2001. Explaining the Rate Spread on Corporate Bonds. The Journal of Finance, 56(1), pp.247-278.
- Elton, E.J., Gruber, M.J., Agrawal, D. and Mann, C., 2004. Factors affecting the valuation of corporate bonds. Journal of Banking & Finance, 28(11), pp.2747-2767.
- Eom, Y.H., Helwege, J. and Huang, J.Z., 2004. Structural models of corporate bond pricing: An empirical analysis. Review of Financial studies, 17(2), pp.499-544.
- Ericsson, J., Jacobs, K. and Oviedo, R., 2009. The determinants of credit default swap premia. Journal of Financial and Quantitative Analysis, 44(1), pp.109-132.
- Fama, E.F. and French, K.R., 1993. Common risk factors in the returns on stocks and bonds. Journal of financial economics, 33(1), pp.3-56.
- Fei, F., Fuertes, A.M. and Kalotychou, E., 2012. Credit rating migration risk and business cycles. Journal of Business Finance & Accounting, 39(1‐2), pp.229-263.
- Foss, G.W., 1995. Quantifying risk in the corporate bond markets. Financial Analysts Journal, 51(2), pp.29-34.
- Frydman, H. and Schuermann, T., 2008. Credit rating dynamics and Markov mixture models. Journal of Banking & Finance, 32(6), pp.1062-1075.
- Grandes, M. and Peter, M., 2005. How Important is Sovereign Risk in Determining Corporate Credit Spreads in Emerging Markets? The Case of Local Currency Bonds in South Africa. IMF Working Paper 217.
- Geske, R.L. and Delianedis, G., 2001. The components of corporate credit spreads: Default, recovery, taxes, jumps, liquidity, and market factors [online] Available at: http://escholarship.org/uc/item/32x284q3 [Accessed on 3 May 2017].
- Hamilton, D.T. and Cantor, R., 2004. Rating transition and default rates conditioned on outlooks. Journal of Fixed Income, 14(2), pp.54-70.
- Hines, M.A., Ang, J.S. and Patel, K.A., 1975. Bond rating methods: Comparison and validation. The Journal of Finance, 30(2), pp.631-640.
- Houweling, P., Mentink, A. and Vorst, T., 2005. Comparing possible proxies of corporate bond liquidity. Journal of Banking & Finance, 29(6), pp.1331-1358.
- Houweling, P. and Vorst, T., 2005. Pricing default swaps: Empirical evidence. Journal of International Money and Finance, 24(8), pp.1200-1225.
- Huang, J.Z. and Huang, M., 2012. How much of the corporate-treasury yield spread is due to credit risk?. Review of Asset Pricing Studies, 2(2), pp.153-202.
- Jarrow, R.A. and Turnbull, S.M., 1995. Pricing derivatives on financial securities subject to credit risk. The journal of finance, 50(1), pp.53-85.
- Jarrow, R.A., Lando, D. and Turnbull, S.M., 1997. A Markov model for the term structure of credit risk spreads. Review of Financial studies, 10(2), pp.481-523.
- Jarrow, R.A., Janosi, T. and Yildirim, Y., 2002. Estimating expected losses and liquidity discounts implicit in debt prices. Journal of Risk, 5(1), pp.1-38.
- Kadam, A. and Lenk, P., 2008. Bayesian inference for issuer heterogeneity in credit ratings migration. Journal of Banking & Finance, 32(10), pp.2267-2274.
- Kaplan, R.S. and Urwitz, G., 1979. Statistical models of bond ratings: A methodological inquiry. Journal of business, pp.231-261.
- Kim, H., K. Ramaswamy, and S. Sunderesan, 1993. Valuation of Corporate Fixed-Income Securities. Financial Management (Special issue on financial distress), 22(3), pp.60-78.
- Kumar, K. and Haynes, J.D., 2003. Forecasting credit ratings using an ANN and statistical techniques. International journal of business studies, 11(1), pp.91-108.
- Lando, D. and Skødeberg, T.M., 2002. Analyzing rating transitions and rating drift with continuous observations. Journal of banking & finance, 26(2), pp.423-444.
- Longstaff, Francis A., and Eduardo S. Schwartz, 1995, A simple approach to valuing risky fixed and floating rate debt. Journal of Finance, 50, pp.789-819.
- Longstaff, F.A., Mithal, S. and Neis, E., 2005. Corporate yield spreads: Default risk or liquidity? New evidence from the credit default swap market. The Journal of Finance, 60(5), pp.2213-2253.
- Manzoni, K., 2004. Modeling Eurobond credit ratings and forecasting downgrade probability. International Review of Financial Analysis, 13(3), pp.277-300.
- Marciniak, M., 2006. Yield curve estimation at the National Bank of Poland; Bank i Kredyt; 10; p. 52-74
- Merton, R., 1974. On the pricing of corporate debt: the risk structure of interest rates. Journal of Finance, (May), 29(2), pp.449-470.
- Nelson, C.R. and Siegel, A.F., 1987. Parsimonious modeling of yield curves. Journal of business, pp.473-489.
- Nickell, P., Perraudin W. and Varotto, S., 2000. Stability of Rating Transitions. Journal of Banking & Finance, 24, pp.203-227.
- Norden, L. and Weber, M., 2009. The co‐movement of credit default swap, bond and stock markets: An empirical analysis. European financial management, 15(3), pp.529-562.
- Wang, Z., 2004. Financial ratio selection for default-rating modeling: a model-free approach and its empirical performance. Journal of Applied Finance, 14(1), pp.20-35.
- Weistroffer, C., Speyer, B., Kaiser, S. and Mayer, T., 2009. Credit default swaps. Deutsche bank research.
- Zhu, H., 2006. An empirical comparison of credit spreads between the bond market and the credit default swap market. Journal of Financial Services Research, 29(3), pp.211-235.
Article Rights and License
© 2018 The Author. Published by Sprint Investify. ISSN 2359-7712. This article is licensed under a Creative Commons Attribution 4.0 International License.


